Bei dieser Aufgabe sollst du ganzrationale Funktionen aufgrund charakteristischer Eigenschaften eines gegebenen Graphen unterscheiden.

Lösung

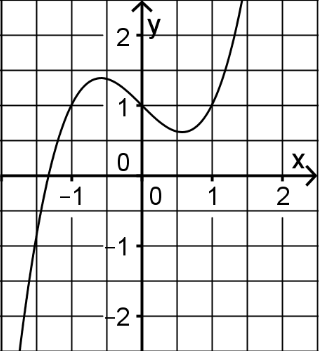
Der abgebildete Graph gehört zur Funktion $g$.

Begründung durch eine Nullstellenbetrachtung:

$g$ hat (mindestens) eine Nullstelle.

$f$ hat keine Nullstelle, da die Diskriminante des quadratischen Funktionsterms negativ ($-3$) ist. Auch $h$ hat keine Nullstelle (positive Summanden wegen geradzahliger Exponenten).

Alternative Begründung durch Betrachtung lokaler Extrema und des Symmetrieverhaltens:

$g$ hat in $ℝ$ (mindestens) zwei lokale Extrema. $f$ hat aber als quadratische Funktion in $ℝ$ genau ein lokales Extremum (den Scheitelpunkt der zugehörigen Parabel).

$h$ ist wegen der geradzahligen Exponenten im Funktionsterm zur y-Achse symmetrisch ($h(x)=h(-x)$). $g$ dagegen nicht.

Bemerkung zu einer eventuellen Entscheidung für $g$ aufgrund des asymptotischen Verhaltens der Funktion für $x$ gegen $\pm \infty$:

Die in Frage kommenden Funktionen $f$, $g$ und $h$ sind in ganz $ℝ$ definiert. Der vorliegende Graph ist aber nur für ein begrenztes Intervall gezeichnet. Ob sich der Graph außerhalb dieses Intervalls nochmals qualitativ ändert, indem z.B. weitere Wendpunkte oder Extrema vorliegen, ist nicht bekannt.

Unter der Annahme, dass dies nicht der Fall ist - aber nur dann - kann man sich auch so für $g$ entscheiden:

Die Funktionswerte von $f$ und $h$ gehen für $x$ gegen $\pm \infty$ wegen des positiven und geradzahligen Leitkoeffizienten in den Funktionstermen gegen $+\infty$. Bei $g$ aber gehen sie gegen $-\infty$ bzw. gegen $+\infty$.

Um das Integral zu berechnen, brauchst du eine Stammfunktion von $h^{\prime }(x)$. Da $h^{\prime }(x)$ die Ableitungsfunktion von $h(x)$ ist, ist $h(x)$ eine Stammfunktion von $h^{\prime }(x)$.

Mit Hilfe des Hauptsatzes der Differential- und Integralrechnung kannst du nun das Integral berechnen:

$${\displaystyle {\int }_0^1{h}^{\prime }(x)dx=[h(x){]}_0^1=[x^4+x^2+1{]}_0^1=(1^4+1^2+1)-(0^4+0^2+1)=3-1=2}$$